Logistics
Time: 4:00-5:00 PM; 3/3/2022
Zoom Link: https://stanford.zoom.us/meeting/register/tJckfuCurzkvEtKKOBvDCrPv3McapgP6HygJ
Presenter
Daniel Russo
Associate Professor of Decision, Risk, and Operations division of Columbia Business School,
Columbia Business School
Abstract
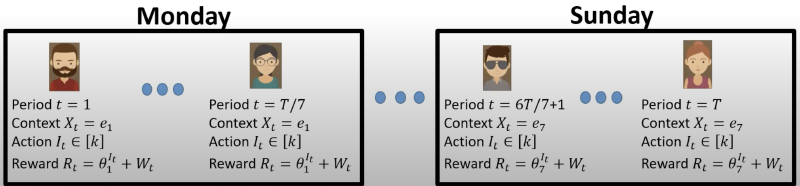
Multi-armed bandit algorithms minimize experimentation costs required to converge on optimal behavior. They do so by rapidly adapting experimentation effort away from poorly performing actions as feedback is observed. But this desirable feature makes them sensitive to confounding, which is the primary concern underlying classical randomized controlled trials. We highlight, for instance, that popular bandit algorithms cannot address the problem of identifying the best action when day-of-week effects may influence reward observations. In response, this paper proposes deconfounded Thompson sampling, which makes simple, but critical, modifications to the way Thompson sampling is usually applied. Theoretical guarantees suggest the algorithm strikes a delicate balance between adaptivity and robustness to confounding. It attains asymptotic lower bounds on the number of samples required to confidently identify the best action -- suggesting optimal adaptivity -- but also satisfies strong performance guarantees in the presence of day-of-week effects and delayed observations -- suggesting unusual robustness. At the core of the paper is a new model of contextual bandit experiments in which issues of delayed learning and distribution shift arise organically.
Reference
https://arxiv.org/pdf/2202.09036.pdf
Bio
Daniel Russo is an Associate Professor in the Decision, Risk, and Operations division of Columbia Business School. His research focuses on problems at the intersection of sequential decision-making and statistical machine learning. He completed his PhD at Stanford under the supervision of Ben Van Roy.